K Means Clustering P.1 – How it Works

K-Means Clustering

K Means clustering is an unsupervised learning algorithm that attempts to divide our training data into k unique clusters to classify information. This means this algorithm does not require labels for given test data. It is responsible for learning the differences between our data points and determine what features determining what class.

Supervised vs Unsupervised Algorithm

Up until this point we have been using supervised machine learning algorithms. Supervised learning means that when we pass training data to our algorithm we also pass the estimated values or classes for each of those data points. For example, when we were classifying the safety of cars we gave the algorithm the features of the car and we told it if the car was safe or not. If we were using an unsupervised algorithm we would only pass the features and omit the class.

How K-Means Clustering Works

The K-Means clustering algorithm is a classification algorithm that follows the steps outlined below to cluster data points together. It attempts to separate each area of our high dimensional space into sections that represent each class. When we are using it to predict it will simply find what section our point is in and assign it to that class.

Step 1: Randomly pick K points to place K centroids Step 2: Assign all of the data points to the centroids by distance. The closest centroid to a point is the one it is assigned to. Step 3: Average all of the points belonging to each centroid to find the middle of those clusters (center of mass). Place the corresponding centroids into that position. Step 4: Reassign every point once again to the closest centroid. Step 5: Repeat steps 3-4 until no point changes which centroid it belongs to.

Visual Example

This example will be done in 2D space with K=2. Meaning two features and two classes. The data we will use is seen below

Step 1: Two random centroids are created and placed on the graph. Step 2: Each point is assigned to a centroid. Step 3: Each centroid is moved into the center of each cluster of points 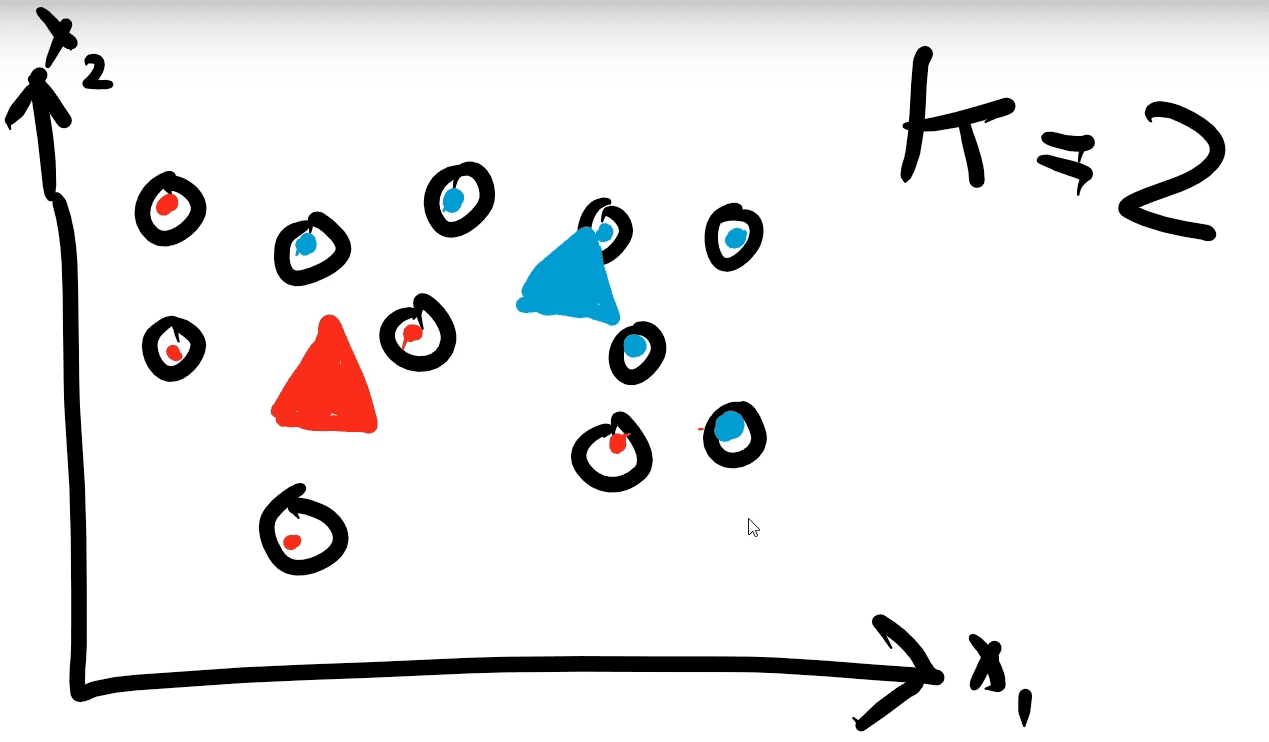Step 4: The points are reassigned to the closest centroids. Step 5: Since each point is already assigned to the closest centroid we do not need to repeat this anymore and our algorithm has finished.